忽然想起来,我这个公众号的tag里还有个计算机相关呢,而我至今还没写过任何关于计算机的东西,正好,人工智能导论复习完了,那就趁此机会写个总结,填补这个公众号的一项空白哈。
这个总结里以学校的练习题中的内容为主,练习题中没提到的内容大概没有,比如规划问题啊隐马尔科夫模型啊什么的。
因为是自己理解的,并不能保证一定正确,若有不正确之处,还请指出。
那么涉及到的内容有:
啥是人工智能
问题描述
路径优化问题(搜索相关的一堆)
约束问题
“优化”
神经网络
估计
信息论
决策树学习
强化学习
受篇幅所限,第一章只涉及到问题描述部分。
后续文章更新时间由我的复习时间决定。
绪
其实,到目前为止(上述内容)所学习的人工智能知识归根结底,是对于搜索问题的深化。
比如问题表述和状态图,其实就是将一个具体时间抽象化,使其能够被数学描述出来,从而使其能够被计算机理解。
中间的内容比如贪婪搜索、A*搜索,是典型的基于“经验公式”的,简单来说,就是if-then的高阶形式。
而后面的从信息论开始,则是通过另一个视角去考虑问题。
那么人工智能和这些东西有什么关系呢?答:上述内容皆为人工智能运行逻辑的解决办法。
那么就很容易理解了,机器学习这个东西,就是人工智能逻辑实现的解决办法,也就是说,到目前为止所涉及到的东西,皆为“机器学习”。
那么,机器学习是什么?
根据数学原理分为两种:
基于经验公式(错误率、边界、代价、风险、实用性、边缘分类等)。例如贪婪搜索,概率估计等;
基于信息理论。“学习的过程就是一个熵减的过程”——学得越多,会的越多,不会的越少=信息的不确定度下降。
其中第一种比较容易理解:给我参数,带入函数得出结果,按结果走。
第二种相对不太容易理解:熵,本质是描述混乱程度的,在信息理论中,就代表着信息的混乱程度,也就是不确定度。熵减,就是信息的不确定性下降。也就是说,信息和熵数量相等,意义相反,获取信息意味着消除不确定性(熵减)。而消除信息的不确定性,本质是正确地调整每个结果可能性的概率。(具体在后面的板块)
问题描述
我们学习人工智能,归根结底是要让机器会解决实际问题,简化一下就是:机器 解决 问题。
好的,机器我们已经有了,这里有一台电脑,那么问题呢?
为了让机器整明白实际问题,我们需要将实际问题抽象化,这时候你就要学会如何正确地“问题表述”了。
在这里我们以非常经典的传教士食人族问题为例:
这有3个传教士和3名食人族要乘船过河(从左到右),船上最多待2人,当一侧传教士少于食人族时,食人族会愉快滴将传教士吃掉。
问,用数学怎么描述这个问题?
首先找到这里面的变量:传教士个数、食人族个数、船的状态。
然后找到由这些变量组成的状态,比如初始状态是,左岸有3个传教士和3个食人族和船,用数学表示就是(b,m,k),其中b={l, r}表示船在左或右侧,m表示传教士的个数,k表示食人族的个数,即初始状态为(l,3,3)。
相对的,我们希望这群人都能过河,那么目标状态显然是(r,3,3)。
同样,这人得乘船过河吧,过河是一种行为,所以这种行为也得用数学表示出来:
从左到右:(m,k) = (1,1) (0,1) (1,0) (2,0) (0,2)
从右到左:(m,k) = (1,1) (0,1) (1,0) (2,0) (0,2)
那么还需要考虑的一个问题是,每次过河有什么代价嘛?
本题比较特殊,因为过河只消耗1次行动的机会,因此消费为1,即cost=1。
此外还需要考虑对于岸的一侧的m和k的人数约束的问题,因为食人族数不能大于传教士数,所以有任意一侧m≥k。
那么左岸有m≥k,右岸有3-m≥3-k,联立一下这俩不等式则有m=k。
那么总结一下,对于此问题的描述就是:
Z = (b, m, k) //状态
b = {l, r} //船的位置
m = k = {0, 1, 2, 3} //人数
m=k
Za = (l, 3, 3)
Zz = (r, 3 ,3)
Aktion = 上面写的10个行为
cost = 1 (也可写成K()=1)
此时问题描述完了,就该去解决问题了。为了解决问题,我们首先得把有效状态都找出来,即符合约束条件的状态,这里我们用排除法:
-当左侧的食人族多于传教士,m<k,(l,2,3),(l,1,2),(l,1,3)
-当右侧的食人族多于传教士,3-m<3-k,(l,2,0),(l,2,1),(l,1,0)
-当船独自位于左岸,(l,0,0)
-当该状态的后一个状态会导致右侧食人族多于传教士时,(l,3,0)
那么刨除这8个状态后,剩余的16个状态便是可行的:
对于b=l有:
(l, 3, 3),(l, 3, 2),(l, 3, 1),(l, 2, 2),(l, 1, 1),(l, 0, 1),(l, 0, 2),(l, 0, 3)
对于b=r, 还需要增加8个状态:
(r, 3, 3),(r, 3, 2),(r, 3, 1),(r, 2, 2),(r, 1, 1),(r, 0, 1),(r, 0, 2),(r, 0, 3)
那么此时根据这16个状态便,根据乘船次序便可以画出状态图了:
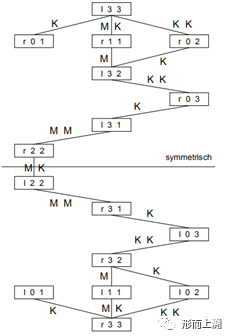
见图,可以发现,我们最终能够到达(r,3,3)的状态,这说明该问题有解,甚至有2x2种不同的解。
思考一下:
-如果有4名传教士和4名食人族,会不会有解呢?
-如果在开始时,让左岸的3名传教士和3名食人族排队上船,船上一次能带2人,有没有解决方案呢?
附加题:如果在中间加个小岛,岛上可以待人,那么对于有相同数量n的传教士和食人族,能否解决问题?
解:首先要明确的一件事是,不论哪一侧,传教士的人数都要多于食人族的人数。所以我们的解决办法就是:利用中间的小岛,使任意一侧的k≥m。
那么,先扔两个食人族到小岛上再说:
左到右k k,把其中一个k扔到岛上,另一个k再划回来
左到右k k,把其中一个k扔到岛上,另一个k再划回来
这时左岸m = n, k = n-2。
接下来:
从左到右M M,都到右岸,其中一个M划回来
从左到右M K,都到右岸,其中的M再划回来
这两个步骤重复n-2次,可以让左岸所有的食人族都到达右岸,且能够保证任意一侧的传教士≥食人族。此时的状态为(l,2,0)
然后剩下的两个传教士一块儿坐船到右岸,再之后派个食人族去接小岛上的两个食人族到右岸,至此全部抵达。
总共渡河次数为:4+4*(n-2)+1+4=4n+1
总结的说,想要完成一个状态描述,包括以下内容:
状态描述
初始状态
目标状态
状态转型(行动)
成本函数
解决问题的方法为画出状态图。
这里给出的算法为正向搜索。不过除了这种搜索方式以外,还有双向搜索,迭代加深搜索,深度搜索,广度优先搜索等,在之后的文章中可能会写吧。
(其实我原本是打算一篇文章写完全部的,结果发现文字量忒大,那就改成分章节吧,下一次更新靠缘分吧。)





Comments NOTHING